Open Library - открытая библиотека учебной информации. Способы преобразования комплексного чертежа Метод замены плоскостей проекций
ОБЩИЕ ПОЛОЖЕНИЯ
СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА
Лекция 4
Решение ряда задач в начертательной геометрии значительно упрощается, когда геометрические фигуры занимают частное положение относительно плоскостей проекций. Задачи на определение взаимного положения фигур и метрические задачи (определение натуральных величин плоскостей, отрезков и т.д.). Для этого существуют различные способы преобразования комплексного чертежа. Каждый из них основан на одном из следующих принципов:
1. на изменении положения плоскостей проекций относительно неподвижных геометрических фигур;
2. на изменении положения заданных геометрических фигур относительно неподвижных плоскостей проекций;
Рассмотрим некоторые из них.
Сущность способа состоит в том, что заданные геометрические фигуры неподвижны в заданной системе плоскостей проекций (П 1 , П 2 ). Последовательно вводятся новые плоскости проекций (П 4 , П 5 ), относительно которых геометрические фигуры займут частное положение. Новая плоскость проекций выбирается с таким расчетом, чтобы она была перпендикулярной к незаменяемой плоскости проекций.
Большинство задач решается с применением одного или двух последовательных преобразований исходной системы плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П 1
(или П 2
), другая плоскость П 2
(или П 1
) должна оставаться неизменной.
На рисунке 1 представлено наглядное изображение метода замены плоскостей проекций. Фронтальная плоскость П 2
заменяется на новую фронтальную плоскость П 4
. Новые проекции точки А
(А 1 А 4
), при этом, как видно из рисунка, высота точки А осталась прежней.
Необходимо запомнить правило построения новых проекций точек при методе замены:
- линии связи всегда перпендикулярны новым осям проекций;
- расстояние от новой оси проекций до новой проекции точки всегда берется с той плоскости, которую заменяют.
Рисунок 1.Наглядное изображение метода замены плоскостей проекций.
Рисунок 2.Изображение метода замены плоскостей проекций на эпюре.
Большинство задач в начертательной геометрии решаются на базе четырех задач:
- Преобразовать прямую общего положения в прямую уровня;
- Преобразовать прямую общего положения в проецирующую прямую;
- Преобразовать плоскость общего положения в проецирующую плоскость;
- Преобразовать плоскость общего положения в плоскость уровня .
Задача №1
Рассмотрим решение задачи №1 . Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.3). Для этого вводим новую фронтальную плоскость проекций П 4 , ось Х 1,4 проводим параллельно А 1 В 1 АВ – А 4 В 4. В новой системе плоскостей проекций прямая АВ – фронталь.
Рисунок 3.
Преобразование прямой общего положения в прямую уровня (фронталь)
Задача №2
Дана прямая АВ – общего положения, преобразуем ее в проецирующую прямую (рис.4). Для решения этой задачи необходимо выполнить последовательно два преобразования:
- Преобразовать прямую общего положения в прямую уровня, то есть решить сначала задачу №1;
- Преобразовать прямую уровня в проецирующую прямую.
Вычертить условие задачи №1, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П 5 Х 4 , 5 перпендикулярно проекции А 4 В 4 и строим новую проекцию прямой А 5 В 5. В системе плоскостей П 4 ,П 5 , прямая АВ является горизонтально проецирующей прямой.
На базе задач №1 и №2 решаются следующие задачи:
1. определение расстояния от точки до прямой;
2. определение расстояния между параллельными и скрещивающимися прямыми;
3. определение натуральной величины прямой;
4. определение величины двугранного угла.
Рисунок 4.
Преобразование прямой общего положения в проецирующую прямую.
Задача №3.
Дана плоскость АВС – общего положения, преобразуем ее в проецирующую плоскость (рис.5). Для решения этой задачи необходимо в плоскости провести линию уровня, если такая отсутствует. Новую ось проекций проводим перпендикулярно лини уровня. В треугольнике АВС проводим горизонталь h. Ось проекций Х 14 проводим перпендикулярно h 1 , новую проекцию плоскости А 4 В 4 С 4 , строим по правилам, разобранным в предыдущих задачах.
В системе плоскостей проекций П 1 ,П 4, плоскость треугольника является фронтально-проецирующей плоскостью.
Рисунок 5.
Преобразование плоскости общего положения в проецирующую плоскость.
Задача №4.
Рисунок 6.
Преобразование плоскости общего положения в плоскость уровня.
Дана плоскость АВС – общего положения, преобразуем ее в плоскость уровня (рис.6). Для решения этой задачи необходимо выполнить последовательно два преобразования:
- Преобразовать плоскость общего положения в проецирующую плоскость, то есть решить сначала задачу №3;
- Преобразовать проецирующую плоскость в плоскость уровня.
Вычертить условие задачи №3, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П 5 , для этого проводим новую ось проекций Х 4 , 5 параллельно проекции А 4 В 4 С 4 и строим новую проекцию треугольника А 5 В 5 С 5. В системе плоскостей П 4 ,П 5 , треугольник АВС является горизонтальной плоскостью уровня.
На базе задач №3 и №4 решаются следующие задачи:
1. определение расстояния от точки до плоскости;
2. определение расстояния между параллельными плоскостями;
3. определение натуральных (истинных) величин геометрических фигур;
определение углов наклона плоскости к плоскостям проекций
Метод плоскопараллельного перемещения
Все вышерассмотренные задачи можно решить используя метод плоско-параллельного перемещения, при котором плоскости проекций остаются на месте, а проекция фигуры перемещается (рис.7).
Рисунок 7. Определение натуральной величины отрезка методом плоско-параллельного перемещения.
Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.7). Для этого перемещаем проекцию А 1 В 1 параллельно оси Х . Строим новую проекцию прямой АВ – А 2 ` В 2 ` , которая будетявляться- натуральной величиной отрезка. Этот метод используется для определения натуральных величин ребер многогранников при построении развертки.
Метод вращения
Частным случаем плоско-параллельного перемещения является метод вращения вокруг проецирующих прямых и прямых уровня.
Часто графическое решение задач существенно упрощается, если заданные плоскости проекций заменить на новые, такие, что в результате замены геометрические объекты займут частное положение.
Сущность способа замены плоскостей проекций заключается в том, что заданные плоскости последовательно заменяются на новые при неизменном положении геометрических объектов в пространстве. Каждая новая плоскость проекций располагается перпендикулярно незаменяемой плоскости проекций.
Важно отметить, что обе заданные плоскости проекций нельзя заменить сразу. Когда требуется замена двух плоскостей проекций, нужно заменить сначала одну, а затем другую, т.е. сделать два преобразования.
При введении новой фронтальной плоскости проекций координаты Z всех геометрических объектов остаются неизменными как в исходной системе плоскостей проекций, так и в новой; при введении новой горизонтальной плоскости проекций неизменными и в исходной, и в новой системе плоскостей проекций остаются координаты Y.
Указанные положения наглядно проиллюстрированы на рис. 37, где показаны преобразования, которые необходимо выполнить при введении (замене) новой плоскости проекций П 4 .
СПОСОБЫ ВРАЩЕНИЯ И ПЛОСКОПАРАЛЛЕЛЬНОГО
ПЕРЕНОСА
Суть метода вращения состоит в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических образов относительно них путем вращения объектов вокруг некоторой оси до тех пор, пока объекты не занимают частное положение в исходной системе плоскостей.
В качестве осей вращения удобнее принимать проецирующие прямые или прямые уровня, причем точки геометрических объектов вращаются в плоскостях, параллельных или перпендикулярных заданным плоскостям проекций. При повороте какого-либо геометрического образа радиус поворота у каждой его точки свой, а угол поворота для всех точек одинаков. На комплексном чертеже при использовании метода вращения принято показывать положение оси вращения.
При вращении вокруг горизонтально-проецирующей прямой i горизонтальная проекция А 1 точки А перемещается по окружности, а фронтальная (А 2) - по прямой, представляющей собой проекцию окружности той плоскости, в которой вращается точка А (рис. 38).

Отметим, что проекции точек на фронтальной плоскости проекций лежат на прямых, перпендикулярных исходным линиям связи. Используя это, можно не задаваться изображением оси вращения и не устанавливать величину его радиуса, на чем и основан метод плоскопараллельного перемещения как частный случай метода вращения. Рассмотрим способ плоскопараллельного переноса на примере решения задачи об определении натуральной величины треугольника ABC (рис. 39).
Решение. Заданный треугольник надо расположить так, чтобы горизонтальная проекция горизонтали плоскости треугольника оказалась перпендикулярной оси X. Поскольку горизонталь плоскости треугольника после такого преобразования станет фронтально-проецирующей прямой, а все горизонтали плоскости параллельны, плоскость треугольника ABC станет фронтально-проецирующей. Сущность следующего преобразования – сделать плоскость треугольника параллельной горизонтальной плоскости проекций. Для этого линию А 2 = В 2 = нужно расположить параллельно оси X. Тогда треугольник A 1 = B 1 = C 1 = станет представлять натуральную величину треугольника ABC.

ЧЕТЫРЕ ИСХОДНЫЕ ЗАДАЧИ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
Подавляющее большинство метрических задач рассматривает прямые и плоскости. Если заранее известно, какие построения нужно выполнить, чтобы прямая (или плоскость) общего положения заняла частное, решение многих метрических задач значительно облегчается.
Частных положений, как у прямой, так и у плоскости - два (прямая (плоскость) уровня и проецирующая). Это означает, что существуют четыре исходные задачи преобразования чертежа, в результате которых: прямая общего положения становится прямой уровня; прямая общего положения становится проецирующей; плоскость общего положения переходит в проецирующую; плоскость общего положения становится плоскостью уровня.
Для решения подобных задач воспользуемся методом замены плоскостей проекций, хотя каждая из них может решаться как способом вращения, так и способом плоскопараллельного переноса.
Задача 1. Преобразовать прямую общего положения (АВ) в прямую уровня (рис. 40). Для решения задачи введем новую фронтальную плоскость проекций П 4 , расположенную параллельно горизонтальной проекции A 1 B 1 прямой (АВ). Т.к. при введении новой фронтальной плоскости проекций координаты Z точек А и В не изменяются, дальнейшие построения ясны из

чертежа, причем проекция А 4 В 4 представляет собой натуральную величину отрезка [АВ]. Таким образом, решение рассмотренной задачи преобразования комплексного чертежа представляет собой еще один способ нахождения натуральной величины отрезка прямой общего положения.
Задача 2. Прямую общего положения необходимо преобразовать в положение проецирующей прямой (рис. 41).
Решение. Задача решается путем двух преобразований, поскольку нужно сделать две замены плоскостей проекций: первой прямая общего положения переводится в положение прямой уровня, а второй полученная прямая уровня переводится в проецирующую. Первое преобразование представляет собой решение рассмотренной выше задачи. Т.к. вводимая во втором преобразовании плоскость проекций (П 5) является новой горизонтальной плоскостью проекций, точка А 5 располагается на линии проекционной связи А 4 А 5 на расстоянии, равном величине координаты Y точки А в системе плоскостей проекций П 1 -П 4 .

Овладев алгоритмом решения приведенной задачи, можно легко найти расстояния между параллельными и скрещивающимися прямыми, от точки до плоскости, а также натуральную величину двугранного угла (представив линию пересечения двух плоскостей в виде проецирующей прямой).
Задача 3. Перевести плоскость общего положения, заданную треугольником ABC, в проецирующую (рис. 42).
Решение. Плоскость, заданная любым способом, представима как множество соответствующих прямых уровня - либо ее горизонталей, либо фронталей. Поэтому преобразования нужно проводить так, чтобы прямые уровня плоскости спроецировались в точки. Тогда плоскость спроецируется в совокупность точек, расположенных на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно горизонтальной проекции горизонтали или фронтальной проекции фронтали плоскости, можно получить соответствующую проецирующую плоскость (рис. 42).
Такой подход позволяет находить расстояния от точки до прямой, между плоскостью и параллельной ей прямой, между параллельными плоскостями.
Задача 4. Плоскость общего положения, заданную треугольником ABC, перевести в положение плоскости уровня (рис. 43).

Решение. Задача решается с помощью двух преобразований. Первым плоскость общего положения переводится в положение проецирующей (решение исходной задачи 3, изложенное выше), а вторым полученная проецирующая плоскость переводится в положение плоскости уровня (на рис. 42 это плоскость горизонтального уровня). Точки А 5 , В 5 и C s расположены от оси X, разделяющей плоскости П 4 и П 5 , на расстояниях, равных величинам координат Y для точек А, В и С в системе плоскостей проекций П 1 -П 4 .
Решение рассмотренной задачи позволяет находить натуральные величины плоских фигур (следовательно, сторон многоугольников и плоских углов). Решение этой же задачи методом плоскопараллельного переноса приведено на рис. 39.
Вопросы
1. Способы преобразования чертежа.
2. В чем заключается способ замены плоскостей?
3. Прямая какого положения используется при определении натуральной величины отрезка способы вращения?
4. Суть плоско-параллельного переноса..
5. сколько раз надо вращать плоскую фигуру вокруг проецирующей прямой для определения натуральной величины?
Тесты к теме « Четыре исходные задачи преобразования чертежа»
1. Как располагается дополнительная плоскость проекций относительно прямой при определении натуральной величины отрезка?
а) параллельно
б) перпендикулярно
в) произвольно
2. Как располагается дополнительная плоскость проекций относительно исходных плоскостей проекций?
а) перпендикулярно одной плоскости проекции
б) перпендикулярно двум плоскостям проекции
в) произвольно
3. Как располагается новая ось относительно проекций отрезка прямой при определении натуральной величины отрезка?
а) параллельно проекции отрезка, расположенной в плоскости перпендикулярной к дополнительной
б) перпендикулярно проекции отрезка, расположенной в плоскости перпендикулярной к дополнительной
в) произвольно
4. Сколько преобразований необходимо для определения натуральной величины плоской фигуры?
5. Сколько необходимо ввести дополнительных плоскостей проекции для преобразования прямой общего положения в проецирующую?
Сущность способа заключается в том, что на чертеже вводится новая плоскость проекций таким образом, что предмет по отношению к ней занимает частное положение.
Рассмотрим применение этого способа к решению четырех основных задач на преобразование.
П е р в а я з а д а ч а: прямая общего
положения преобразуется в прямую уровня (рис. 5.1).
Чтобы преобразовать прямую AB общего положения в прямую уровня, необходимо ввести новую плоскость проекций параллельно АВ, т. е. на чертеже провести новую координатную ось параллельно А 1 В 1 или А 2 В 2 . В рассматриваемом случае координатная ось П 1 проведена параллельно А 1 В 1 , таким образом введена новая фронтальная плоскость проекций. Для построения проекции отрезка на этой плоскости нужно из А 1 и В 1 провести линии связи, перпендикулярные координатной осиП 1 /П 4 .
Так как высота прямой в пространстве не изменилась, то от оси П 1 /П 4 на соответствующих линиях связи откладываем высоту точек А и В, получаем А 4 и В 4 . Проекции прямой А 1 В 1 и А 4 В 4 дают положение прямой АВ, параллельное новой фронтальной плос-
кости проекций. Проекция А 4 В 4 – натуральная величина отрезка АВ. Угол между натуральной величиной прямой и горизонтальной проекцией – это угол наклона АВ к горизонтальной плоскости проекций П 1 . Если есть необходимость определить угол наклона прямой АВ к фронтальной плоскости проекций, тогда координатную ось П 2 /П 5 необходимо провести параллельно А 2 В 2 и на линиях связи от этой оси отложить А у и В у.
Угол между натуральной величиной и фронтальной проекцией и есть угол (β) наклона прямой АВ к П 2 .
Часто для определения натуральной величины отрезка и углов наклона прямой к плоскостям проекций пользуются способом прямоугольного треугольника, который является следствием из решения первой задачи на преобразование (рис. 5.2).
Натуральная величина отрезка есть гипотенуза прямоугольного треугольника, один катет которого – сама проекция отрезка, другой катет по величине является разностью координат концов отрезка, взятой на другой плоскости проекций.
В т о р а я з а д а ч а: прямая уровня преобразуется в прямую проецирующую (рис. 5.3).
Для решения этой задачи необходимо новую плоскость проекций провести перпендикулярно натуральной величине прямой А 1 В 1 . Проекции А 1 В 1 и А 4 В 4 дают положение прямой АВ, перпендикулярное новой фронтальной плоскости проекций П 4 .
Т р е т ь я и ч е т в е р т а я з а д а ч и: плоскость общего положения преобразуется в плоскость проецирующую, и плоскость проецирующая – в плоскость уровня.
Решение этих двух задач приведено на рис. 5.4. Пусть дана плоскость общего положения – задана треугольником АВС. Чтобы преобразовать ее в проецирующую, нужно ввести новую плоскость проекций перпендикулярно треугольнику АВС, но на комплексном чертеже это возможно в том случае, если провести плоскость проекций перпендикулярно линиям уровня или следам плоскости.
С этой целью проведем в плоскости треугольника АВС горизонталь. Перпендикулярно h 1 проведем координатную ось (П 1 /П 2). Прямая уровня h преобразовалась в прямую проецирующую h(h 1 h 4). Из проекции вершин треугольника А 1 ,В 1 ,С 1 проведем линии связи и от (П 1 /П 4) отложим соответствующие координаты А 2 ,В 2 ,С 2 . Проекция треугольника А 4 ,В 4 ,С 4 представляет собой прямую линию.
Таким образом, плоскость общего положения преобразована в плоскость проецирующую. Угол между проекцией треугольника А 4 В 4 С 4 и координатной осью является углом наклона плоскости к П 1 .
Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П 1 или П 2 новой плоскостями П 4 (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.
Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1 : Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П 4 , параллельно отрезку АВ и перпендикулярно плоскости П 1 . Введением новой плоскости, переходим из системы плоскостей П 1 П 2 в систему П 1 П 4 , причем в новой системе плоскостей проекция отрезка А 4 В 4 будет натуральной величиной отрезка АВ .
Задача 2 : Определить расстояние от точки А до прямой общего положения, заданной отрезком ВС (рис._149).


Понятие многогранника.
Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.
Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.
Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.
Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамидой. Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды. Общая вершина треугольников называется особой вершиной пирамиды (обычно, просто вершиной).
Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду.
Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.
Под изображением многогранников на чертеже будем понимать изображение ограничивающей его многогранной поверхности, т.е. изображение совокупности составляющих ее многогранников. Графически простую многогранную поверхность удобно задавать проекциями ее сетки.
Построение проекций:
Построение проекций многогранников
Построение проекции многогранника на некоторой плоскости сводится к построению проекций точек. Например, проецируя пирамиду SABC на пл.я 2 (рис. 256, слева), мы строим проекции вершин S, А, В и С и, как следствие, проекции основания ABC, граней SAB, SBC, SAC, ребер SA, SB и др.
Также, проецируя трехгранный угол ") с вершиной S (рис. 256, справа), мы, помимо вершины S, берем на ребрах угла по одной точке (К, М, N) и проецируем их
на пл. я 2 ; в результате получаем проекции ребер и граней (плоских углов) трехгранного угла и В целом самый угол.
На рис. 257 изображены многогранное тело ACBB 1 D... (т. е. часть пространства, ограниченного со всех сторон плоскими фигурами - многоугольниками) и его проекция на пл. я 1 - фигура A"C"F . Заменим плоскость V на V 1 (V 1 H)(V 1 )x 1 x 1 x 1 B 2 B x =B x1 B 4 A 2 A x =A x1 A 4 |А 4 B 4 |=|АB|- угол наклона АВ к плоскости Н.
Решение второй задачи: Заменим плоскость Н на Н 1 (Н 1 V 1)(H 1 )x 2 A x2 A 5 =B x2 B 5 =A 1 A x1 =B 1 B x1
|
|
Таким преобразованием можно решать задачи об определении истинной величины отрезка и углов наклона его к плоскостям проекций.
Совместное рассмотрение первой и второй задач позволяет решать задачи об определении:
расстояния от точки до прямой
расстояния между двумя параллельными прямыми
расстояния между скрещивающимися прямыми
Третья задача: Заменить плоскость проекций так, чтобы плоскость общего положения стала проецирующей плоскостью.
Четвёртая задача: Заменить плоскость проекций так, чтобы проецирующая плоскость стала плоскостью уровня.
Решим обе задачи совместно:
Решение третьей задачи: Пусть задана плоскость общего положения Р(ABC) Заменим V на V 1 (V 1 H)(V 1 P) x 1 - угол наклона плоскости Р к плоскости Н.

 Календари природы серия «Окружающий мир
Календари природы серия «Окружающий мир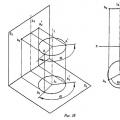 Способы преобразования комплексного чертежа Метод замены плоскостей проекций
Способы преобразования комплексного чертежа Метод замены плоскостей проекций К чему снится шкаф - толкование сна
К чему снится шкаф - толкование сна